Números amigáveis são pares de números onde um deles é a soma dos divisores do outro.
Por exemplo, os divisores de 220 são 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110, cuja soma é 284.
Por outro lado, os divisores de 284 são 1, 2, 4, 71 e 142 e a soma deles é 220. Fermat descobriu também o par 17.296 e 18.416. Descartes descobriu o par 9.363.584 e 9.437.056.
O recorde de maior primo de Fermat generalizado conhecido: 16717632768+1, que tem 171153 dígitos foi descoberto por Yves Gallot (este é o oitavo maior primo conhecido atualmente, e maior primo conhecido que não é de mersenne
Você sabe quantas casas decimais do número Pi são conhecidas?
São conhecidas 51539600000 casas decimais de Pi, calculadas por Y. Kamada e D. Takahashi, da Universidade de Tokio em 1997. Em 21/8/1998 foi calculada pelo projeto Pihex a 5000000000000a. casa binária de Pi.
O maior número primo conhecido é 232.582.657-1, que tem 9.808.358 dígitos e foi descoberto em 4/9/2006 pelos Drs. Curtis Cooper, Steven Boone e sua equipe. Este primo tem 650.000 dígitos a mais do que o maior primo encontrado por eles mesmos em dezembro de 2005.
| O maior par de primos gêmeos conhecido é 2003663613 . 2195000+/-1. Esses primos têm 58711 dígitos, e foram descobertos em janeiro de 2007 |
|
| | Um número é capicua quando lido da esquerda para a direita ou da direita para a esquerda representa sempre o mesmo valor, como por exemplo 77, 434, 6446, 82328. Para obter um número capicua a partir de outro, inverte-se a ordem dos algarismos e soma-se com o número dado, um número de vezes até que se encontre um número capicua, como por exemplo:
Partindo do número 84: 84+48=132;132+231=363, que é um número capicua.
Outra forma de calcular potências
|
Pitágoras descobriu que existe outra forma de calcular potências: através da soma de números ímpares. Ele descobriu que n2 é igual a soma dos nprimeiros números naturais ímpares. Exemplo:
52 = 1+3+5+7+9 = 25 |
Você conhece o número mágico?
1089 é conhecido como o número mágico. Veja porque:
Escolha qualquer número de três algarismos distintos: por exemplo, 875.
Agora escreva este número de trás para frente e subtraia o menor do maior:
875 - 578 = 297
Agora inverta também esse resultado e faça a soma:
297 + 792 = 1089 (o número mágico)
Aviso: antes que você nos envie um e-mail dizendo que não funciona com determinados números, lembramos que devem ser usado três dígitos no cálculo. Exemplo:
574 - 475 = 099
099 + 990 = 1089
Uma curiosidade com números de três algarismos.
Escolha um numero de três algarismos:
Ex: 234
Repita este numero na frente do mesmo:
234234
Agora divida por 13:
234234 / 13 = 18018
Agora divida o resultado por 11:
18018 / 11 = 1638
Divida novamente o resultado, só que agora por 7:
1638 / 7 = 234
O resultado é igual ao numero de três algarismos que você havia escolhido: 234.
Você sabe o que são números triangulares?
Os primeiros números triangulares são 1, 3 e 6. Veja por que:
Os números triângulares podem ser calculados através de duas fórmulas: a iterativa e a recursiva:
Fórmula iterativa
T(n) = 1+2+3+...+n
Fórmula recursiva
T(1) = 1
T(n+1) = T(n)+(n+1)
Os números cíclicos são aqueles que multiplicados por outro número menor ou igual ao número de dígitos de que ele possui, seus números vão se repetindo ciclicamente, passando para o final aqueles que estão na frente. Por exemplo: O primeiro número cíclico é o 142857. Se este número (que possui seis dígitos) for multiplicado pelos números de 1 a 6 obtemos:
2 x 142857 = 285714 (note que o 1 e o 4 foram passados para o final)
3 x 142857 = 428571 (o 1 passa para o final)
4 x 142857 = 571428
5 x 142857 = 714285
6 x 142857 = 857142
Se multiplicarmos por 7 o que obtemos é 999999. Isto não é uma casualidade. Esse número (142857) é a parte periódica da divisão 1/7.
O próximo número cíclico é o 0588235294117647. Se multiplicarmos este número pelos números de 1 a 16 acontece o mesmo que com o anterior. Se o multiplicarmos por 17 resulta em 99999999999999999.
Esses números são raros de encontrar. Outra cracterística curiosa destes números é a forma que se pode obtê-los:
Pegamos um número primo e calculamos seu inverso (1/p). Se a parte decimal é periódica e o período possui tantos dígitos quanto o número primo menos 1, então este é um número cíclico. Quando dividimos 1/7 se obtém 0,142857142857142857. Note que é periódico e que o período possui seis dígitos.
|
| O número PI representa o valor da razão entre a circunferência de qualquer círculo e seu diâmetro. É a mais antiga constante matemática que se conhece. É um número irracional, com infinitas casas decimais e não periódico. |
São números inteiros da forma Mp = 2p -1. Se Mp é um número primo, o numero p também é. Só são conhecidos 33 números de Mersenne. O último descoberto corresponde a p= 859 433, cujo número de Mersenne é o 2859433 -1.
Não se sabe se há um número infinito deles.
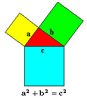
São os inteiros que cumprem a equação de Pitágoras a2 + b2 = c2 . Por exemplo: 3, 4 e 5
| Um número natural é chamado de ascendente se cada um dos seus algarismos é estritamente maior do que qualquer um dos algarismos colocados à sua esquerda. Por exemplo, o número 3589. |
Quadrados perfeitos e suas raízes
Os pares de quadrados perfeitos:
144 e 441, 169 e 961, 14884 e 48841
e suas respectivas raízes:
12 e 21, 13 e 31, 122 e 221, são formados pelos mesmos algarismos, porém escritos em ordem inversa.
O matemático Thébault investigou os pares que têm esta curiosa propiedade. Encontrou, por exemplo, a seguinte dupla:
11132 = 1.238.769 e 31112 = 9.678.321
Curiosidade com números triangulares
|
Se um número triangular é multiplicado por 8 e acrescido de 1, o resultado é um número quadrado.
Veja:
1.8 + 1 = 9
3.8 + 1 = 25
Essa afirmação foi feita por Plutarco aproximadamente no ano 100 D.C.
O maior número aceito no sistema de potências sucessivas de dez, é ocentilhão, registrado pela primeira vez em 1852. Representa a centésima potência de um milhão, ou o número 1 seguido de 600 zeros (embora apenas utilizado na Grã-Bretanha e na Alemanha).
O quadrado de um numero é um dos inteiros da série 1, 4, 9, 16, 25, etc. Não se torna difícil verificar a relação entre os membros consecutivos desta série. Verificamos que se somarmos o quadrado de x , mais duas vezes x mais 1 , o próximo quadrado sucessivo é obtido.
Por exemplo , 52 + 2.5 + 1 = 25+10+ 1 = 36 = 62
Se soubermos o valor de um determinado número ao quadrado, o próximo numero é facilmente obtido.
Exemplo: Sabendo que o quadrado de 18 é 324 , temos:
192 = 182 + 2.18 + 1 = 324+36+ 1 = 361
A razão para tal fato verifica-se pela relação algébrica:
(a + b)2 = a2 + 2ab + b2
19 = (18 + 1) = 182 + 2.18.1 + 12 = 361
Um número é dito regular se sua decomposição em fatores primos apresenta apenas potências de 2, 3 e 5.
Exemplo:
60 é um número regular, pois 60= 2².3.5.
Quadrado da soma dos números naturais
|
(1 + 2 + 3 + 4)2 = 13 + 23 + 33 + 43
100 = 1 + 8 + 27 + 64
O quadrado da soma de uma série de números naturais começando por 1 é igual à soma do cubo de suas parcelas
| Este número, multiplicado por 1, 2, 3, 4, 5, 6, 8 ou 9, tem como resultado outro número cujos algarismos estão na mesma ordem do original. Mas se o resultado tiver 7 algarismos ao invés de 6, basta somar o primeiro com o último número para se obter novamente a seqüência. Veja:
142857 x 5 = 714285
142857 x 8 = 1142856, somando os extremos (1 + 6) = 7 -> 714285
O melhor de tudo é que você não precisa pegar o 142857, pode pegar qualquer número com os 6 algarismos nessa sequencia, que todos eles têm essa propriedade. Veja:
428571 x 2 = 857142
285714 x 3 = 857142
285714 x 9 = 2571426, somando os extremos (2 + 6) = 8 -> 857142
E se você multiplicar qualquer desses números que têm esses algarismos nessa sequência por 7 ou por um múltiplo de 7, você encontrará uma seqüência de 9. E novamente se houverem mais de 6 algarismos, quase todos serão 9, os que não forem, somados darão 9. Veja:
857142 x 7 = 5999994 (5 + 4 = 9)
571428 x 49 = 27999972 (2 + 7 = 9)
714285 x 14 = 9999990 (9 + 0 = 9)
Se multiplicarmos o número 12345679 por qualquer múltiplo de 9, entre 9 e 81, iremos obter um produto cujo algarismo que se repete é o próprio multiplicador dividido por 9.
12345679 x 9 = 111.111.111 (9 / 9 = 1)
12345679 x 18 = 222.222.222 (18 / 9 = 2)
12345679 x 27 = 333.333.333 (27 / 9 = 3)
12345679 x 36 = 444.444.444 (36 / 9 = 4)
12345679 x 45 = 555.555.555 (45 / 9 = 5)
12345679 x 54 = 666.666.666 (54 / 9 = 6)
12345679 x 63 = 777.777.777 (63 / 9 = 7)
12345679 x 72 = 888.888.888 (72 / 9 = 8)
12345679 x 81 = 999.999.999 (81 / 9 = 9)
Data histórica: 20/02 de 2002 |
|
|
Quarta-feira, dia 20 de fevereiro de 2002 foi uma data histórica. Durante um minuto, houve uma conjunção de números que somente ocorre duas vezes por milênio.
Essa conjugação ocorreu exatamente às 20 horas e 02 minutos de 20 de fevereiro do ano 2002, ou seja, 20:02 20/02 2002.
É uma simetria que na matemática é chamada de capicua (algarismos que dão o mesmo número quando lidos da esquerda para a direita, ou vice-versa). A raridade deve-se ao fato de que os três conjuntos de quatro algarismos são iguais (2002) e simétricos em si (20:02, 20/02 e 2002).
A última ocasião em que isso ocorreu foi às 11h11 de 11 de novembro do ano 1111, formando a data 11h11 11/11/1111. A próxima vez será somente às 21h12 de 21 de dezembro de 2112 (21h12 21/12/2112). Provavelmente não estaremos aqui para presenciar.
Depois, nunca mais haverá outra capicua. Em 30 de março de 3003 não ocorrerá essa coincidência matemática, já que não existe a hora 30.
Gugol é o número 1 seguido de 100 zeros.
Esse nome surgiu quando em certa ocasião, o matemático americano Edward Kasner perguntou ao seu sobrinho de 9 anos, Milton Sirotta, qual era o maior número que existia. A resposta do menino (algo como guuugol) não foi muito animadora, mas na mente de Kasner isso virou uma bela brincadeira. Em homenagem ao sobrinho, ele chamou de gugol ("googol", em inglês) o número 1 seguido de 100 zeros ou, dizendo de outra forma, o número 10 elevado a 100.
Em seguida, usou o gugol como base para denominar um número ainda maior: o gugolplex, que equivale a "10 elevado a 1 gugol". Imagine quantas folhas de papel seriam necessárias para escrever o número gugolplex por entenso...
|
Você sabia que a diferença de um número com o outro que obtemos escrevendo-o de trás para frente é igual a zero ou a um múltiplo de nove? Veja alguns exemplos:
22 - 22 = 0
51 - 15 = 36 (múltiplo de 9)
444 - 444 = 0
998 - 899 = 99 (múltiplo de 9)
1350 - 0531 = 819 (múltiplo de 9)
654321 - 123456 = 530865 (múltiplo de 9)
A diferença entre o PHI e o Pi é muito mais que só o 'H'. O número PHI, representado pelo número 1,618 é muito importante na arte. O PHI é geralmente considerado o número mais belo do mundo. Este número vem da série de Fibonacci - uma progressão famosa não só porque a soma dos termos adjacentes equivalia ao termo seguinte, mas porque os quocientes dos termos adjacentes possuíam a estarrecedora propriedade de irem se aproximando gradativamente do número 1,618, o PHI!
Apesar das origens matemáticas aparentemente místicas do PHI, o aspecto surpreendente do PHI foi seu papel como componente básico na Natureza. Plantas, animais e até seres humanos - todos possuíam propriedades dimensionais que se encaixavam com uma exatidão espantosa à razão de PHI para um. A unipresença do PHI na natureza está além da coincidência, e assim os antigos presumiram que o número PHI deve ter sido predeterminado pelo Criador do universo. Os primeiros cientistas solenemente anunciaram que o número um vírgula seis um oito era a Divina Proporção.
Exemplos:
1) Se você dividir o número de abelhas fêmeas pelo número de abelhas machos em qualquer colméia do mundo, vai sempre obter o mesmo número: PHI, 1,618.
2) Um miolo de flor de girassol. As sementes de girassol crescem em espirais opostas. A razão de cada rotação para a seguinte é de 1,618, PHI.
Leonardo Da Vince foi o primeiro a demonstrar que o corpo humano é literalmente feito de componentes cujas razões proporcionais sempre equivalem a PHI.
3) Se você dividir a distância que vai do alto da cabeça até o chão, depois dividir o resultado pela distância do umbigo até o chão, vai obter 1,618, PHI.
4) A distância de um ombro até a ponta dos dedos dividido pela distância entre o cotovelo até a ponta dos dedos. PHI, 1,618.
* Curiosidade enviada pelo usuário Leonardo Magalhães.
Obtendo um quadrado perfeito
Você sabia que adicionando o número 1 à multiplicação de quatro números consecutivos você obtém um quadrado perfeito?
Exemplo: 1*2*3*4+1 = 25
* Curiosidade enviada pelo usuário Isaac Farias.
Existem diversos provérbios que envolvem o número dois. Exemplos:
"Mais vale um pássaro do que dois voando".
"Homem avisado vale por dois".
"Matar dois coelhos numa cajadada só".
"Mais vale um toma do que dois te darei".
"Dois proveitos não cabem num saco só".
"Entre os dois venha o diabo e escolha".
"Criados e bois, um ano até dois".
"Custa mais sustentar um vício do que educar dois filhos".
"Duas mudanças equivalem a um incêndio".
"Duas vezes perdido o que ao ingrato é concebido".
"Mais vale um hoje do que dois amanhã".
"Mais vale um pé do que duas muletas".
"Mais valem duas pernas do que três andas".
"Não há dois altos sem um baixo no meio".
"Dois pilotos fazem um barco ir ao fundo".
"Dois sacos vazios não se põe em pé".
"Dois sentidos não assam milho".
"Dois sobre um asno, sinal de bom amigo".
"Dois pesos e duas medidas".
|
|
Sudoku é um game divertidíssimo e viciante, que está virando febre no mundo inteiro. O objetivo do jogo é completar um grid (colunas verticais e linhas horizontais), preenchendo os espaços vazios com números de 1 a 9. O segredo: o número não pode ser repetido na mesma coluna, linha ou bloco. Veja a seguir um exemplo de Sudoku, com sua respectiva solução:
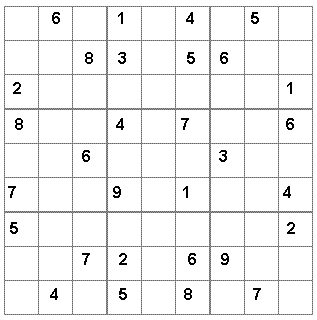
Solução:
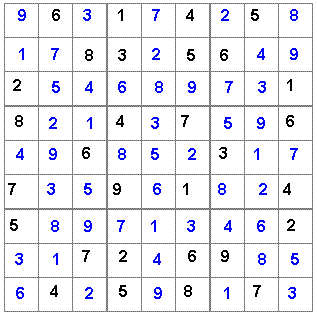
Clique aqui para fazer o download do Sudoku Solver, um software que resolve o quebra-cabeças.
Terno, referindo-se a vestuário, designava o conjunto de três peças: calça, paletó e colete. Por este motivo que é chamado terno. Porém, hoje ele é constituído de duas peças: calça e paletó.

Existem diversos provérbios que envolvem o número três. Exemplos:
"Três vezes na cadeia é sinal de forca."
"Quem vai à festa três dias não presta."
"Três coisas mudam o homem: Vinho, estudo e mulher."
"Segredo de três o diabo fez."
"Três irmãos, três fortalezas."
"Companhia de três é má rês."
"Segredo de dois, segredo de Deus; segredo de três, o diabo fez."
"Um é pouco, dois é bom, três é demais."
"O peixe deve nadar três vezes: em água, em molho, em vinho!"
"Por mal não se leva um português, por bem dois ou três."
"Fortuna de lobo três dias dura."
"A mulher, o fogo e os maus são males."
"Pão de quinze dias, fome de três semanas."
"A sebe dura três anos; o cão, três sebes; o cavalo, três cães; o homem, três cavalos; o corvo, três homens e o elefante, três corvos."
"O hóspede e o peixe aos três dias aborrecem."
"Três à carga, carga ao chão."
"Três mulheres e um pato fazem uma feira."
"Três luzes a arder deitam uma casa a perder."
Existem diversas coleções que totalizam cinco elementos. Veja alguns exemplos:
- Cinco, os dedos da mão
- Cinco, os dedos do pé
- Cinco, os títulos mundias da seleção brasileira de futebol
- Cinco, as pétalas de uma rosa
- Cinco, são os sentidos
- Cinco, as vogais
- Cinco, as pontas de uma estrela
- Cinco, os rios do Inferno
- Cinco, as ordens nobres da arquitetura
- Cinco, os mandamentos de Buda
- Cinco, os capitães famosos da história
- Cinco, as linhas da pauta musical
- Cinco, as grandes eras geológicas
- Cinco, os poliedros regulares convexos
Você sabia que os dermatologistas definiram uma fórmula para calcular, aproximadamente, a área da superfície corporal de uma pessoa? A área (em m2) é calculada em função da massa (m) do indivíduo:
Por exemplo, uma pessoa com massa igual a 70kg possui a área da superfície corporal aproximadamente igual a:
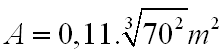
O valor resultante é útil para determinar a quantidade de calor perdida através do suor. |
Existem diversas palavras derivadas do vocábulo quatro. Além dos números quatrocentos, quatrilão, quadragésimo, entre outros, podemos citar:
Quadrilátero - polígono de quatro lados.
Quadrante - arco correspondente à quarta parte da circunferência.
Quadrúpede - que possui quatro pés.
Quarteto - trecho de música executado por quatro vozes ou por quatro instrumentos. No caso do quarteto vocal, as vozes que completam são: soprano, contralto, tenor e baixo.
Quatríduo - espaço de quatro dias.
Quaresma - é o espaço de quarenta dias (desde a quarta feira de cinzas), sem contar os domingos, que precedem o domingo da Páscoa. Esse período é consagrado a orações e jejum pelos católicos.
Quartilho - a quarta parte de uma camada.
Quadriênio - período de quatro anos.
Quádruplo - multiplicado por quatro; quatro vezes maior.
Quadricelular - que é dividido em quatro células.
Quadriga - veículo antigo puxado por quatro cavalos.
 Decodificando a mensagem Decodificando a mensagem |
|
| Leia e decodifique a mensagem abaixo:
4S V3235 3U 4C0RD0 M310 M473M471C0.
D31X0 70D4 4 4857R4Ç40 N47UR4L D3 L4D0
3 M3 P0NH0 4 P3N54R 3M NUM3R05,
C0M0 53 F0553 UM4 P35504 R4C10N4L.
540 5373 D1550, N0V3 D4QU1L0...
QU1N23 PR45 0NZ3...
7R323N705 6R4M45 D3 PR35UNT0...
M45 L060 C410 N4 R34L
3 C0M3Ç0 4 F423R V3R505
H1NDU-4R481C05
Mágica com o calendário
Peça a uma pessoa que, em um mês qualquer do calendário, ela delimite um “quadrado” 3 por 3, contendo 9 dias quaisquer. Veja o exemplo de uma escolha no calendário abaixo para o mês agosto de 2005.
Agosto 2005
|
|---|
| Dom | Seg | Ter | Qua | Qui | Sex | Sab |
|---|
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 | | | |
Depois, peça que ela informe qual é a menor data do quadrado, e diga que com apenas essa data você irá descobrir a soma de todas as datas escolhidas. Para isso, você deve somar a menor data (no caso, 10) com 8 e multiplicar o resultado por 9.
Ou seja, (10 + 8) x 9 = 18 x 9 = 162
(ou seja, 10 + 11 + 12 + 17 + 18 + 19 + 24 + 25 + 26 = 162).
|
|
|
|
|
|
Pegue 5 moedas e peça para uma pessoa organizá-las da forma que ela quiser (cara ou coroa voltada para cima). Por exemplo:
    
Veja que, nesse exemplo, foram escolhidas 3 coroas e 2 caras. Agora vire-se de costas e peça para a pessoa virar quantas moedas ela quiser. Cada vez que ela virar uma moeda, ela deve dizer a palavra "VIREI".
Quando encerrar, peça para a pessoa colocar a mão sobre uma das moedas. Agora você vai virar de frente novamente, e dizer se a moeda que está embaixo da mão da pessoa é CARA ou COROA! Quer saber como?
O TRUQUE: antes de virar-se de costas, conte o número de coroas. No exemplo são 3, ou seja, é um número ímpar. Toda vez que a pessoa disse a palavra "VIREI", o número de coroas troca de ímpar para par ou de par para ímpar. Por exemplo, na situação acima, se a pessoa disser "VIREI" três vezes, teremos:
1ª vez - nº de coroas par
2ª vez - nº de coroas ímpar
3ª vez - nº de coroas par
Ao virar-se de frente, a pessoa estará com a mão sobre uma das moedas, mas você estará vendo as outras quatro. Então, em nosso exemplo, basta ver se o número de coroas que você está vendo é par. Se não for, a moeda que está embaixo da mão é COROA. Caso contrário, é CARA.
Vamos ilustrar nosso exemplo para que você entenda melhor. Imagine que, das moedas do desenho acima, viramos a primeira e a segunda. Então teríamos:
    
Como foram viradas 2 moedas, o número de coroas deve continuar sendo ímpar. Por exemplo, se a pessoa colocar a mão sobre a quarta moeda:
   ? ? 
Você saberá que a moeda que falta é CARA, pois já existe um número ímpar (1) de coroas.
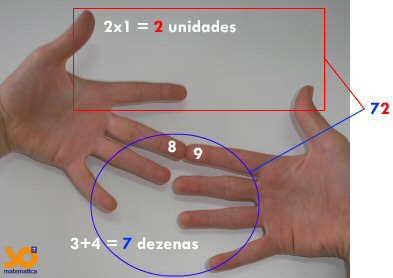
Você sabia que pode utilizar os dedos para realizar multiplicações entre números de 6 a 10? Para isso, é necessário identificar os dedos da seguinte forma:
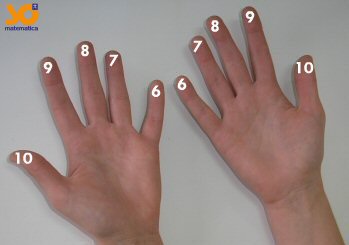
Por exemplo, para calcular 8x9, encosta-se o dedo equivalente ao 8 no dedo equivalente ao 9 na outra mão, como mostra a figura abaixo.

O resultado será um número de dois dígitos, onde o dígito das dezenas será igual à soma dos dedos que estiverem abaixo (incluindo os que estão em contato), e o dígito das unidades será igual à multiplicação dos dedos que estiverem acima. A figura a seguir ilustra a multiplicação.
|
|
|
|
|
|
|

Peça para a pessoa, com uma calculadora:
1º) Digitar os 4 primeiros números de telefone dela;
2º) Multiplicar por 80;
3º) Somar 1;
4º) Multiplicar por 250;
5º) Somar os 4 últimos números do telefone dela;
6º) Somar mais uma vez os 4 últimos números do telefone dela;
7º) Subtrair 250;
8º) Dividir 2.
O resultado será o telefone dessa pessoa! Veja um exemplo:
Telefone 3663-3645
1º) 3663 x 80 = 293040
2º) 293040 + 1 = 293041
3º) 293041 x 250 = 73260250
4º) 73260250 + 3645 = 73263895
5º) 73263895 + 3645 = 73267540
6º) 73267540 - 250 = 73267290
7º) 73267290 / 2 = 36633645
Resultado: 36633645
|
|
|
Solicita a alguém que pense no número do mês de seu nascimento (Janeiro 1, Fevereiro 2, Março 3...). Em seguida peça-lhe que:
1) multiplique o número por 2
2) some 5 ao resultado
3) multiplique por 50
4) some sua idade ao resultado
Após a pessoa lhe informar o resultado, você deve subtrair 250. Os dois últimos números do resultado final darão a idade da pessoa, enquanto o primeiro número (ou primeiros números) será o mês de nascimento. Com essa informação, fica fácil determinar o ano.
Por exemplo, para uma pessoa que tem 20 anos e nasceu em janeiro, teríamos as seguintes operações:
1) Multiplica-se 1 (janeiro) por 2 => 1*2 = 2
2) Soma-se 5 => 2+5 = 7
3) Multiplica-se por 50 => 7*50 = 350
4) Soma-se a idade => 20+350 = 370
Subtrai-se 250 => 370-250 = 120
De 120, o primeiro número revela o mês (janeiro), e os dois últimos (20) são a idade da pessoa. Basta então deduzir o ano, de acordo com a data em que se faz a demonstração.
A raiz quadrada de números seqüenciais ascendentes e descendentes é sempre igual ao número 1 na quantidade expressa pelo maior algarismo contido nesse número.
EXEMPLOS:
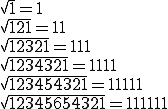
Considerando o dia 4 de Maio de 2006, aos 2 minutos e 3 segundos passados da 1 hora da manhã, temos o seguinte horário seqüencial:
01:02:03 04/05/06
É uma seqüencia numérica que jamais irá se repetir.
Sabemos que o ângulo reto mede 90º e que o ângulo raso mede 180º. Mas por que motivo os valores são 90 e 180?
No ano de 4000 a.C., os egípcios e árabes tentavam elaborar um calendário. Nessa época, se acreditava que o Sol levava 360 dias para completar a órbita de uma volta em torno da Terra. Assim, a cada dia o Sol percorria um pouquinho dessa órbita, ou seja, um arco de circunferência de sua órbita. Esse ângulo passou a ser uma unidade de medida e foi chamado de grau.
Então, para os antigos egípcios e árabes, o grau era a medida do arco que o Sol percorria em torno da Terra durante um dia. Porém, hoje sabemos que é a Terra que gira em torno do Sol, mas se manteve a tradição e se convencionou dizer que o arco de circunferência mede um grau quando corresponde a 1/360 dessa circunferência.
Lemniscata é o nome do símbolo do infinito, o conhecido "oito deitado", ou um "laço simples".
Esta palavra tem origem do latin e significa "Laços Simétricos".
Tabuada do nove com os dedos
|

Esta é uma maneira simples de efetuarmos multiplicações (de 1 a 10) por 9. Devemos considerar os dedos contando da esquerda para a direita e numerando-os seqüencialmente de 1 a 10. Então, basta baixarmos o dedo correspondente ao número que queremos multiplicar por 9, e teremos o resultado.
Por exemplo: 4x9. Baixamos o dedo correspondente ao numero 4. Repare que ficaram 3 dedos do lado esquerdo e 6 dedos do lado direito do dedo baixado. Agora é só unir o 3 e o 6, ou seja, o resultado é 36.*
Enviado pelo usuário Alessandro Fonseca de Araújo
 Quais são os quadrados perfeitos? Quais são os quadrados perfeitos? |
|
|
|
Começando do zero, some a seqüência de ímpares e a resposta será um quadrado perfeito.
Ex: Começando do 0, somamos o primeiro número ímpar positivo, o 1. Encontramos o quadrado perfeito 1. Agora somamos o próximo número ímpar, o 3. E assim sucessivamente.
0 + 1 = 1
1+ 3 = 4
4 + 5 = 9
9 + 7 = 16
16 + 9 = 25
25 + 11 = 36
36 + 13 = 49
...
|
Um ano é bissexto quando ele é divisível por 4. Porém, existe uma exceção. Os anos que terminam por dois zeros serão bissextos se forem divisíveis por 400.
Exemplo:
2012 é um ano bissexto. Pois 2012 / 4 = 503, ou seja, uma divisão exata.
1998 não é um ano bissexto, pois 1998 / 4 = 499,5, uma divisão inexata.
5000 não é um ano bissexto pois, apesar de ser divisível por 4, é um número terminado em 00 e não é divisível por 400.
Primeiro, faça uma coluna de 0 a 9:
0
1
2
3
4
5
6
7
8
9
Depois, faça uma coluna de 9 a 0:
9
8
7
6
5
4
3
2
1
0
Agora, junte as duas para obter os resultados da tabuada do nove:
09
18
27
36
45
54
63
72
81
90
* Enviado por Gabriel Pires Zampol
Um pentagrama é uma estrela composta por cinco retas e que possui cinco pontas.
Podemos enxergá-la como uma estrela feita pela união dos pontos de um pentágono regular.
Na língua portuguesa, pentagrama significa uma palavra com cinco letras.
Um século começa em um ano 01 e termina em um ano 00.
Por exemplo, o século XX começou em 1901 e terminou em 2000 e o século XXIcomeçou em 2001 e terminará em 2100.
No entanto, para alguns, que reconhecem as alterações feitas ao calendário Gregoriano em 1582, um século começa em um ano 00 e acaba em um ano 99.
Os séculos na História são numerados com algarismos romanos e nomeados com ordinais do I até o IX (primeiro, segundo, terceiro...) e com cardinais do X em diante (dez, onze, doze, treze...).
|
|
|
Texto enviado pelo usuário Eudes Antonio, relacionando a idade de uma pessoa à vontade que ela tem de comer chocolate.
|
Confira as probabilidades que você possui de ganhar na Mega Sena, de acordo com a quantidade de números jogados.
Números jogados
|
Probabilidade de Acerto (1 em ...)
|
Sena
|
Quina
|
Quadra
|
6
|
50.063.860
|
154.518
|
2.332
|
7
|
7.151.980
|
44.981
|
1.038
|
8
|
1.787.995
|
17.192
|
539
|
9
|
595.998
|
7.791
|
312
|
10
|
238.399
|
3.973
|
195
|
11
|
108.363
|
2.211
|
129
|
12
|
54.182
|
1.317
|
90
|
13
|
29.175
|
828
|
65
|
14
|
16.671
|
544
|
48
|
15
|
10.003
|
370
|
37
|
|
Muitas pessoas perguntam por que a páscoa de 2008 aconteceu tão cedo. De fato, a Páscoa de 2008 aconteceu mais cedo do que qualquer um de nós irá ver durante nossas vidas!
A última vez em que isso ocorreu foi em 1913. A próxima vez que a Páscoa ocorrerá em 23 de março, será no ano 2228. Logo, não estaremos aqui para presenciar (pelo menos nesta vida, para os que pensaram em reencarnação).
E será que a Páscoa pode acontecer mais cedo ainda? Pode sim! No ano de 2285, ela ocorrerá no dia 22 de março!
Mas afinal, qual é a data correta da Páscoa? Ela acontece sempre no primeiro domingo após a lua cheia, depois do equinócio de março. Durante o ano, acontecem dois equinócios, sendo o primeiro no dia 21 de março e o segundo no dia 23 de setembro. São os dois únicos dias do ano nos quais o dia tem exatamente a mesma duração, em horas, minutos e segundos, que a noite.
A Páscoa é sempre o primeiro Domingo depois da primeira lua cheia, depois do equinócio de Primavera. A data baseia-se no calendário lunar que o povo hebreu usava para identificar a Páscoa judaica, razão pela qual a Páscoa é uma festa móvel no calendário romano.
Em diversos idiomas europeus, a palavra "noite" assemelha-se à junção da letra "n" com o número 8. Veja alguns exemplos:
Português: noite = n + oito
Inglês: night = n + eight
Alemão: nacht = n + acht
Espanhol: noche = n + ocho
Francês: nuit = n + huit
Italiano: notte = n + otto
|
Os caracteres numéricos que usamos hoje têm uma origem árabe (provavelmente marroquina) e têm mais de mil anos. Uma possível explicação histórica é a de que a erosão provocada pelo uso alterou-os ligeiramente, mas a idéia original parece ter uma explicação curiosa:
O "1" tem um ângulo
O "2" tem dois ângulos
O "3" tem três ângulos
...
O "0" tem zero ângulos!
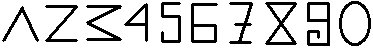
|
Os camponeses russos, segundo alguns matemáticos, utilizavam um processo curioso de multiplicação.
Vamos ver um exemplo, no qual iremos obter o produto do número 36 pelo número 13.
Escrevemos os dois fatores (36 e 13), um ao lado do outro:
36 --------- 13
Determinamos a metade do primeiro e o dobro do segundo, escrevendo os resultados abaixo dos fatores correspondentes:
36 -------- 13
18 -------- 26
Procedemos do mesmo modo com os resutados obtidos:
36 --------13
18 -------- 26
9 --------- 52
Novamente, repetimos a operação. Como chegamos a um número ímpar (que no caso é 9), devemos subtrair uma unidade e tomar a metade do resultado. De 9, subtraindo 1 ficamos com 8, cuja metade é 4. Procedemos desta forma até chegarmos ao termo igual a 1 na coluna à esquerda.
Temos, portanto:
36 ------- 13
18 ------- 26
9 -----52 (X)
4 ------ 104
2 -------208
1 --- 416 (X)
Somando os números da coluna à direita que correspondem aos números ímpares da coluna à esquerda (ou seja, os que marcamos com um X), teremos:
52 + 416 = 468
O resultado obtido (468) será o produto do número 36 por 13.
Você sabia que, se alguém contasse em voz alta até um milhão, 24 horas por dia, sem parar - 1... 2... 3... - dizendo um algarismo ou número por segundo, gastaria nada menos que 12 dias para terminar a enumeração?
A tradição matemática ocidental, durante longo tempo, atribuiu a descoberta deste teorema a Pitágoras. Pesquisas históricas mais recentes constataram que o teorema era conhecido pelos babilônios, cerca de 1500 a.C., portanto muito tempo antes de Pitágoras. Os chineses o conheciam talvez por volta de 1100 a.C. e os hindus provavelmente cerca de 500 a.C.
Referências
Boyer, C.B., História da Matemática. São Paulo, Editora Edgard Blücher, 1996.
Eves, H., Introdução à História da Matemática. Campinas, Editora da UNICAMP, 1995.
 Multiplicação de 37 por múltiplos de 3 Multiplicação de 37 por múltiplos de 3 |
|
|
|
Ao multiplicarmos 37 por múltiplos de 3 menores que 30, nos deparamos com uma fato curioso:
3 x 37 = 111
6 x 37 = 222
9 x 37 = 333
12 x 37 = 444
15 x 37 = 555
18 x 37 = 666
21 x 37 = 777
24 x 37 = 888
27 x 37 = 999
|
|
|
|
 Superstição em torno do número 13 Superstição em torno do número 13 |
|
|
|
Você sabe qual a origem da superstição em torno do número 13? Na mitologia nórdica, encontramos uma lenda sobre o assunto.
Odin, chefe de uma tribo asiática, estabeleceu na Escandinávia seu reino. Para administrá-lo, celebrar os rituais religiosos e predizer o futuro, Odin teria escolhido doze sábios, reunindo-os em um banquete no Valhalla, morada dos deuses. Loki, o deus do fogo, apareceu sem ser convidado e armou uma grande confusão. Como invejava a beleza radiante de Balder, deus do Sol e filho de Odin, fez com que Hodur, o deus cego, o assassinasse por engano. Daí veio a crendice de que 13 pessoas reunidas para um jantar é desgraça certa.
Essa lenda é semelhante, ao episódio da Ultima Ceia de Cristo: Segundo alguns relatos, participaram dessa ceia sagrada os doze apóstolos e Cristo, num total de 13 pessoas. Também aí o final foi infeliz: a crucificação e morte de Cristo, numa sexta-feira. E mais. Na antiga numeração hebraica, os números eram representados por letras. A letra que indicava a quantidade treze era a mesma usada para a palavra morte.
|
|
O sinal de X, que indicamos na multiplicação, foi empregado pelo matemático inglês Guilherme Oughtred no livro Clavis Matematicae, publicado em 1631. Ainda nesse mesmo ano, Harriot, para indicar também o produto a efetuar, colocava um ponto entre os fatores.
Em 1637, Descartes já se limitava a escrever os fatores justapostos, indicando, desse modo abreviado, um produto qualquer. Na obra de Leibniz, escontra-se o sinal 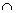 para indicar multiplicação. Esse mesmo símbolo, colocado de modo inverso, indicava a divisão. O ponto foi introduzido como um símbolo para a multiplicação por Leibniz.
As formas a/b e 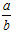 , indicando a divisão de a por b, são atribuídas aos árabes. A razão entre duas quantidades é indicada pelo sinal : , que apareceu em 1657 numa obra de Oughtred. O sinal 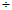 , segundo Rouse Ball, resultou de uma combinação de dois sinais existentes - e :
|
O costume de dar o nome de Bhaskara para a formula de resolução da equação do segundo grau é aparentemente brasileiro (não se encontra o nome Bhaskara para essa fórmula na literatura internacional).
Porém, problemas envolvendo equações do segundo grau já apareciam, há quase quatro mil anos, em textos escritos pelos babilônios. Esses textos possuiam uma receita (escrita em prosa, sem uso de símbolos), que ensinava como proceder para determinar as raízes.
Além disso, até o fim do século 16, não se usava uma fórmula para obter as raízes de uma equação do segundo grau, simplesmente porque não se representavam por letras os coeficientes de uma equação. Isso começou a ser feito a partir de François Viete, matemático francês que viveu de 1540 a 1603.
Logo, embora não se deva negar a importância e a riqueza da obra de Bhaskara, não é correto atribuir a ele a conhecida formula de resolução da equação do segundo grau.
|
O emprego regular do sinal + (mais) aparece na Aritmética Comercial de João Widman d'Eger, publicada em Leipzig em 1489. Entretanto, os sinais de mais e de menos não representavam a adição ou a subtração, ou os números positivos ou negativos, mas os excessos e os déficit em problemas de negócio (Cajori vol. 1, página 128).
Os símbolos positivos e negativos vieram somente ter uso geral na Inglaterra depois que foram usados por Robert Recorde, em 1557. Todavia, já eram usados antes de aparecerem na escrita. Por exemplo: foram pintados em tambores para indicar se os tambores estavam cheios ou não.
Os antigos matemáticos gregos, como se observa na obra de Diofanto, limitavam-se a indicar a adição juntapondo as parcelas - sistema que ainda hoje adotamos quando queremos indicar a soma de um número inteiro com uma fração. Como sinal de operação mais usavam os algebristas italianos a letra P, inicial da palavra latina plus.
Você sabia que já existiu um Papa matemático?
Gerbert, geômetra famoso, foi arcebispo de Ravena e subiu à Cátedra de São Pedro no ano 999. Considerado um dos mais sábios do seu tempo, chamou-se Papa Silvestre II. Foi o primeiro a vulgarizar no Ocidente latino o emprego dos algarismos arábicos.
Além da matemática, dedicou-se ao estudo da astronomia, física, bem como outras ciências, sob o domínio Muçulmano na Espanha. Faleceu em 1003.
|
|
Esta é uma brincadeira que você pode enviar por e-mail aos seus amigos. Copie o texto abaixo, colocando o seu nome no item 9. Quando seus amigos fizerem o cálculo para descobrirem seus ídolos, o resultado dará sempre 9, ou seja, você será sempre o ídolo escolhido.
Se queres saber quem admira, faça este pequeno exercício:
1) Escolha um número de 1 a 9
2) Multiplique por 3
3) Some 3
4) Volte a multiplicar por 3
5) Some os dois dígitos do resultado
Agora olhe mais abaixo...
v
v
v
v
v
v
v
v
v
Com o resultado do cálculo, busque seu ídolo na seguinte lista:
1. Einstein
2. Nelson Mandela
3. Abraham Lincoln
4. Bill Gates
5. Obama
6. Gandhi
7. George Clooney
8. Thomas Edison
9. [COLOQUE AQUI SEU NOME]
10. Oprah Winfrey |
A Sociedade Brasileira de Educação Matemática (SBEM) elegeu o dia 6 de maio “DIA NACIONAL DA MATEMÁTICA”, em memória da data de nascimento de Júlio César de Mello e Souza, o MALBA TAHAN.
Neste dia, fica a sugestão de promover, em todos os estados brasileiros, a realização de eventos comemorativos, com o objetivo de difundir a Matemática como área do conhecimento, sua História, possíveis relações com as demais áreas, e de colocar em discussão algumas crenças sobre o ensino atual de Matemática.
|
Roberto Record, matemático inglês, terá sempre o seu nome apontado na história da Matemática por ter sido o primeiro a empregar o sinal = ( igual ) para indicar igualdade.
No seu primeiro livro, publicado em 1540, Record colocava o símbolo 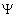 entre duas expressões iguais; o sinal =, constituído por dois pequenos traços paralelos, só apareceu em 1557. Comentam alguns autores que, nos manuscritos da Idade Média, o sinal = aparece como uma abreviatura da palavra est.
Guilherme Xulander, matemático alemão, indicava a igualdade , em fins do século XVI, por dois pequenos traços paralelos verticais; até então a palavraaequalis aparecia, por extenso, ligando os dois membros da igualdade.
Os sinais > ( maior que ) e < ( menor que ) são devidos a Thomaz Harriot, que muito contribuiu com seus trabalhos para o desenvolvimento da análise algébrica.
O número primo 73939133 tem uma propriedade muito estranha. Se você remover os dígitos do final, os números obtidos também são primos. Observe:
73939133 é um número primo
7393913 é um número primo
739391 é um número primo
73939 é um número primo
7393 é um número primo
739 é um número primo
73 é um número primo
7 é um número primo
|
|
Antigos pastores, para controlar seus rebanhos de ovelhas, os associavam a pedras que guardavam em sacolas. Cada ovelha correspondia a uma pedrinha. No início e final do dia, faziam as devidas correspondências. Se sobrasse pedra, faltava ovelha. Como pedrinha em latim significa "Calculus", daí vem a palavra cálculo.
Vários filmes trazem a Matemática como temática. Seguem alguns deles:
- Quebrando a banca” (EUA, 2008), de Robert Luketic.
- "A Prova" (EUA, 2005), de John Madden.
- "Uma Mente Brilhante" (EUA, 2005), de Ron Howard.
- “Enigma” (EUA, 2001), de Michael Apted.
- “Pi” (EUA, 1988), de Darren Aronofsky.
- “Gênio Indomável” (EUA, 1997), de Gus Van Sant.
- “Cubo” (Canadá, 1997), de Vincenzo Natali.
|
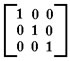
Faz pouco mais de 150 anos que as matrizes tiveram sua importância detectada e saíram da sombra dos determinantes. O primeiro a lhes dar um nome parece ter sido Cauchy, 1826: tableau ( = tabela ).
O nome matriz só veio com James Joseph Sylvester, 1850. Seu amigo Cayley, com sua famosa Memoir on the Theory of Matrices, 1858, divulgou esse nome e iniciou a demonstrar sua utilidade.
Ele usou o significado coloquial da palavra matriz, qual seja: local onde algo se gera ou cria. Com efeito, via-as como "...um bloco retangular de termos...o que não representa um determinante, mas é como se fosse uma MATRIZ a partir da qual podemos formar vários sistemas de determinantes, ao fixar um número p e escolher à vontade p linhas e p colunas..." (artigo publicado naPhilosophical Magazine de 1850, pag 363-370).
Note que Sylvester ainda via as matrizes como um mero ingrediente dos determinantes. Somente com Cayley que elas passam a ter vida própria e gradativamente começam a suplantar os determinantes em importância.
Um número inteiro n é simpático quando existem inteiros positivos a, b e c, tais que:
a<b<c e n = a2 + b2 - c2.
Por exemplo:
- 1 é um número simpático, pois 1 = 42 + 72 - 82.
- 3 é um número simpático, pois 3 = 42 + 62 - 72.
No ano 830, Mohamed Ben Musa Alkarismí, um dos sábios mais notáveis do Século IX, fazia subtrações de números inteiros da seguinte forma:
(Para que você possa acompanhar as operações, usaremos aqui algarismos modernos.)
De 12025 vamos tirar 3604.
A operação era iniciada pela esquerda (operação I). Assim, a 12 tirava 3 e restavam 9; cancelava os algarismos considerados (12 e 3) e escrevia o resto obtido em cima do "minuendo".
Continuando: a 90 tirava 6 restavam 84. A diferença obtida (operação II) era escrita sobre o "minuendo" e os algarismos que formavam os termos de subtração eram cancelados.
Por fim, a 8425 tirava 4 e restavam 8421 (operação III).
E assim temos a diferença entre os números dados.
A palavra seno é derivada do latim sinus, que significa "baía" ou "dobra", a partir de uma tradução errônea (via árabe) do sânscrito jiva, e sua variante jya.
Aryabhata usou o termo ardha-jiva ("meia-corda"), que foi abreviado para jiva e então transliterada pelos árabes como jiba.
Tradutores europeus como Robert of Chester e Gherardo of Cremona, na Toledo do século XII, confundiram jiba com jaib, que significa "baía", provavelmente porque jiba e jaib são escritas da mesma forma na escrita arábica (esse sistema de escrita, em uma de suas formas, não fornece ao leitor informações completas sobre as vogais).
|
|
|
É natural suspeitarmos que o triângulo aritmético não seja uma invenção de Pascal. A denominação desse triângulo varia muito ao longo do mundo.
Os franceses o chamam triângulo de Pascal. Os chineses o chamam de triângulo de Yang Hui. Os italianos o chamam de triângulo de Tarataglia. Encontramos ainda outras denominações, como triângulo de Tartaglia-Pascal ou simplesmente triângulo aritmético ou triângulo combinatório.
As ideias sobre o triângulo aritmético foram redescobertas e introduzidas várias vezes e em todos os locais onde se estudou ou estuda Matemática.
O Brasil ganhou a copa do mundo em 1994. Antes disso, sua última conquista do título foi em 1970. Se você somar, 1970 + 1994 = 3964.
A Argentina ganhou a copa do mundo em 1986, antes em 1978. Somando, 1978 + 1986 = 3964.
Já a Alemanha ganhou a copa em 1990. Antes disso, foi em 1974. Somando 1990 + 1974 = 3964.
O Brasil ganhou a copa do mundo de 2002, e também foi o vencedor da copa de 1962. Conferindo: 1962 + 2002 = 3964.
Seguindo essa lógica, o ganhador da Copa de 2010 será o mesmo que em 1954. Somando: 1954 + 2010 = 3964.
E a Copa do Mundo em 1954 foi vencida pela Alemanha.
Será que esta numerologia irá funcionar?
Resultado: não funcionou, mas chegou perto! A Alemanha caiu na semifinal :)
Logicamente, a conhecida linguagem de programação Pascal não foi criada pelo grande matemático Blaise Pascal, visto que ela foi idealizada no ano de 1971, ou seja, mais de 300 anos após a morte de Pascal. Porém, foi batizada dessa forma em homenagem a ele.
O idealizar da linguagem foi Niklaus Wirth, professor da Faculdade Politécnica de Zurique, na Suíça. Seu objetivo era desenvolver uma linguagem de programação disciplinada para ensinar programação estruturada. No fundo, trata-se de uma versão simplificada para propósitos educacionais da linguagem Algol, que data de 1960.
Quando a linguagem Pascal foi criada, muitas linguagens de programação já existiam, mas poucas eram usadas em larga escala: FORTRAN, C, Assembler, COBOL. A linguagem Pascal só ganhou popularidade quando foi adotada pela Universidade da Califórnia, San Diego, em 1973.
|
O cálculo diferencial e integral, que Newton desenvolve ao mesmo tempo que o alemão Wilheim Leibniz (1646-1716), revoluciona a matemática.
Para se saber a área de um círculo, utilizando a nova ferramenta, basta dividir esse círculo em quadrados iguais, bem pequenos. Em seguida, calcula-se a área de um quadrado e multiplica-se pelo número total de quadrados. Com isso, acha-se a área (ou o volume, se for o caso) de qualquer figura.
Os quadrados têm de ser infinitamente pequenos para encher toda a borda do círculo, e o número de quadrados precisa ser infinito. Portanto, a área total será uma soma de infinitos termos, tipo de soma que os gregos já sabiam fazer há mais de 2 mil anos.
|
A trigonometria não é obra de um só homem ou nação. A sua história tem milhares de anos e faz parte de todas as grandes civilizações.
Percebe-se que, desde os tempos de Hiparco até os tempos modernos, não havia "razão" trigonométrica. Ao invés disso, os gregos e depois os hindus e os muçulmanos usaram linhas trigonométricas. Essas linhas primeiro tomaram a forma de cordas e mais tarde meias cordas, ou senos.
Depois, essas cordas e linhas de senos seriam associadas a valores numéricos, possivelmente aproximações, e listados em tabelas trigonométricas.
|
|
Atualmente, definimos números primos como aqueles que possuem apenas 4 divisores: + ou - ele mesmo, +1 e -1.
Porém, quando foram pensados pela primeira vez, muito provavelmente por Pitágoras, cerca de 530 ac, a palavra primo não tinha relação de parentesco, mas sim de primário.
A ideia de números primários, introduzida por Pitágoras, continua até hoje. Para Pitágoras, existiam os números primários e os números secundários. De maneira simplificada, os números primários ou primos são aqueles que não podem ser obtidos por multiplicação de outros números, e os secundários são aqueles que podem ser gerados pela multiplicação de outros números.
Ao longo do tempo, os números primos também foram denominados de retilíneos, lineares e eutimétricos.
Faça A = 100, B = 101, C = 102, e assim sucessivamente até Z = 125.
Agora some os números para o nome HITLER.
H
|
107
|
I
|
108
|
T
|
119
|
L
|
111
|
E
|
104
|
R
|
117
|
107 + 108 + 119 + 111 + 104 + 117 = 666
De acordo com a tradição cristã, o número 666 correspondente ao sinal da Besta.
|
|
O ano de 2011 possui quatro datas incomuns: 1/1/11, 1/11/11, 11/1/11, 11/11/11.
E tem mais: pegue os últimos 2 dígitos do ano em que você nasceu + a idade que você vai ter este ano, quando fizer aniversário, e a soma será igual a 111 para todos!
|
O volume da Terra é aproximadamente de 1 sextilhão de metros cúbicos. Para observar o movimento da Terra, os cientistas criam sistemas computacionais que analisam a Terra dividindo-a em cubos. Neste caso, tomando cubos de 1 quilometro de aresta, o sistema deverá analisar 1 trilhão de cubos. Por esta imensidão de cálculos matemáticos, é difícil a previsão de terremotos.
O terremoto de 2011 que afetou o Japão, apontado na Escala Richter em 8,9, equivale à intensidade da explosão de quase 1 bilhão de caminhões carregados com 32 toneladas de explosivos TNT.
Observe este número: 21578943.
Note que ele apresenta todos os dígitos significativos, menos o 6. Agora o multiplique por 6.
21578943 x 6 = 129473658
Veja que no resultado aparecem todos os dígitos significativos, inclusive o 6. Ou seja, a multiplicação, por ser gentil, possibilitou a entrada do dígito 6 no número anterior.
Segundo dados levantados pelo IBGE, se o Brasil fosse um país com 100 pessoas, a cada grupo de 100 pessoas o país teria:
- 18 analfabetos funcionais;
- 16 trabalhadores da área rural;
- 20 casais;
- 51 mulheres;
- 50 pessoas da classe C;
- 28 pessoas com telefones residenciais;
- 7 negros;
- 74 católicos;
- 10 graduados em alguma faculdade;
- 42 moradores do Sudeste.
|
Observe o desenvolvimento mental precoce de alguns dos grandes matemáticos.
Blaise Pascal, aos 16 anos de idade, escreveu um tratado sobre as cônicas, considerado como um dos fundamentos da geometria moderna. Pascal contribuiu decisivamente para a criação de dois novos ramos da matemática: a Geometria Projetiva e a Teoria das Probabilidades.
Évariste Galois, aos 15 anos, discutia e comentava as obras de Legendre e Lagrange, o que culminou, posteriormente, na percepção da impossibilidade de encontrar um expressão para raízes de equações algébricas com grau maior que 4.
Alexis Clairaut, aos 10 anos, lia e compreendia as obras do Marquês de L'Hôpital sobre cálculo. E acabou sendo o precursor da Geometria Diferencial.
Joseph Bertrand, aos 11 anos, iniciava o curso na escola Politécnica, e aos 17 recebia o grau de doutor. Aos 23 anos, lançou a conjectura que sempre existe ao menos 1 número primo entre n e 2n-2 para todo n maior do que 3.
Nicolas Henri Abel, aos 16 anos de idade, fazia investigações sobre o problema de resolução da equação do quinto grau, o que desencadeou, posteriormente, na primeira prova completa da inexistência de uma fórmula algébrica para essas raízes. Morreu aos 26 anos de tuberculose.
Johann Carl Friedrich Gauss, aos 7 anos de idade, somou os números inteiros de 1 a 100 rapidamente usando o raciocínio que demonstra, até hoje, a fórmula da soma de uma progressão aritmética.
Aqui, no Hotel de Hilbert, sempre há vagas!
Em 1925, Hilbert apresentou um paradoxo do infinito que ficou mais conhecido como o Hotel de Hilbert.
Neste hotel há infinitos hóspedes e está lotado, mas sempre que chega algum cliente o gerente solicita que os hóspedes pulem de quarto, mudando-se para o quarto ao lado. Assim:
O hóspede do quarto 1 pula para o quarto 2
O hóspede do quarto 2 pula para o quarto 3
...
O hóspede do quarto n pula para o quarto n+1
Logo, o paradoxo está na ideia de que, apesar de sempre estar lotado, no Hotel de Hilbert sempre há vagas.
Muitas coincidências mostram a relação do número 13 com o Papa João Paulo II.
- Tornou-se papa aos 58 anos de vida (5+8=13)
- Seu pontificado durou 9301 dias (9+3+1=13)
- Sofreu um atentado no dia 13 de maio.
- Faleceu na 13ª semana do ano.
- Quando faleceu tinha 85 anos (8+5=13)
- Data de sua morte: 02/04/2005 (2+4+2+5=13)
- Hora de sua morte: 21h37min (2+1+3+7=13)
- Ele foi o 265º papa (2+6+5=13)
As antenas parabólicas têm o formato de uma curva chamada parábola, que está associada ao gráfico da função do segundo grau.
Definimos parábola a partir de uma reta r e um ponto F, chamado foco, em um plano. A parábola de foco F e diretriz r é o conjunto de todos os pontos cuja distancia à reta r é igual à distancia ao ponto F.
Como os sinais que recebemos de rádios ou de luz são muito fracos, quando "captados" pela parábola, ela os concentra em um único ponto, o foco, que os amplia naturalmente, para depois serem refletidos.
Os números deficientes foram introduzidos por Nicomachus na Introductio Arithmetica.
São aqueles cuja soma dos seus divisores próprios é menor do que esse número. Por exemplo, 14 é um número deficiente, pois:
14 > 1+2+7=10
As operações inversas da potenciação são: a radiciação e a logaritmação.
Isso ocorre porque na operação de potenciação não existe a propriedade de comutatividade. Por exemplo:
53 = 5 x 5 x 5 = 125
é diferente de
35 = 3 x 3 x 3 x 3 x 3 = 243
Por definição, a operação inversa à potenciação consiste em: dada a potência e um dos dados, a base ou o expoente deve determinar o outro.
Então:
Dadas a potência e o expoente, se queremos a base devemos usar aRADICIAÇÃO.
Dadas a potência e a base, se queremos o expoente devemos usar aLOGARITMAÇÃO.
No dia 30 de junho de 2012, os relógios foram atrasados 1 segundo, ou seja, o mês de junho teve 1 segundo mais.
Os cientistas explicam esta ingerência no tempo da Terra pela necessidade de adaptação, mediante o acréscimo de 1 segundo “bissexto”, ao ritmo da rotação do nosso planeta.
Segundo a edição britânica, esta foi a 25ª ingerência no tempo na Terra.
O que é mais firme? Uma cadeira de 3 pés ou uma cadeira de 4 pés?
Você já percebeu que muitas vezes uma cadeira de 4 pés fica bamba? Isso não acontece com uma cadeira de 3 pés, que sempre será mais firme. Isso ocorre porque três pontos não alinhados sempre irão determinar um plano. Já quando temos uma cadeira com 4 pés, temos quatro pontos que poderão determinar até quatro planos. Como pode se apoiar em qualquer um deles, a cadeira poderá ficar “dançando”. Nesse caso, a solução seria colocar um calço em um dos pés, para que ele fique contido no mesmo plano dos demais.
|
|
- Se dormirmos, em média, 8 horas por dia, aos 40 anos teremos dormido 13 anos.
- O esqueleto de um homem de 64 quilos pesa cerca de 11 quilos.
- Uma pessoa pisca os olhos aproximadamente 25 mil vezes por dia.
- Se as doenças do coração, o câncer e os diabetes fossem erradicados, a expectativa de vida do homem seria de 99,2 anos.
- As unhas da mão crescem aproximadamente 4 vezes mais rápido que as do pé.
- Os pés possuem um quarto dos nossos ossos.
- 7 minutos é o tempo médio em que uma pessoa normal demora a adormecer.
- Se não exercitarmos o que aprendemos, esquecemos 25% em seis horas, 33% em 24 horas e 90% em seis meses.
- Com uma média de 70 batidas por minuto, o coração bate 37 milhões de vezes por ano.
Conhecer a quantidade de pessoas em um determinado local é importante para o Poder Público, pois assim poderá planejar o policiamento, estimar a necessidade real de profissionais das diversas áreas - médicos, enfermeiros, bombeiros, infra-estrutura, e ainda, quantidade de copos de água, ambulância e outros benefícios.
Este cálculo é fácil de fazer, bastando para isso uma simples operação matemática. Sabe-se que um metro quadrado (m²) pode ser ocupado por nove pessoas, no máximo, nas grandes concentrações.
As concentrações são divididas em três categorias: pequena, média e grande. Na concentração pequena, calculam-se três pessoas por metro quadrado; na média, seis pessoas; e na grande nove pessoas por metro quadrado.
Multiplicando-se o número médio de participantes por m² pela área útil ocupada, chegar-se-á ao número médio de pessoas presentes numa reunião. Eis a regra:
N P m² x A (m²) = T P A
Sendo:
N P m² = número de pessoas por m²;
A = área ocupada em m²;
T P A = Número total de pessoas na área.
Exemplo hipotético: O cantor Roberto Carlos fará um show em um espaço livre de 100 metros de comprimento por 60 metros de largura. Qual a capacidade de espectadores em pé neste local?
Temos os seguintes dados:
Número de pessoas por metro quadrado = 9
Area quadrada do local? 100 x 60 = 6000 m²
Resolvendo o problema 9 x 6000 = 54000.
Logo, 54000 é o número máximo de pessoas em pé que o local comporta.
Com apenas um olhar você pode ter o público aproximado. Se a quantidade de pessoas for como a de uma decisão de campeonato de futebol, multiplica-se a área quadrada por nove. Se você achar que tem muita gente, mas percebe muito espaço vazio, multiplique por 6. E assim sucessivamente.
Fonte: adaptado de abocadopovo.com.br
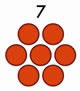
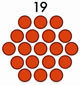
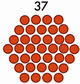
Sabemos que um número hexagonal é aquele que pode ser representado na forma de um hexágono, como por exemplo o número 6:
No entanto, existem também os números hexagonais centralizados, que são aqueles que podem ser dispostos em forma de hexágono, começando com um ponto no meio. Exemplos:
Olhe para as imagens abaixo. A primeira é um vaso, certo? E a segunda? Você acreditaria que são duas pessoas, olhando uma para a outra?
Este é o famoso vaso de Rubin, uma ilusão de óptica desenvolvida pelo psicólogo dinamarquês Edgar Rubin. A ilusão apresenta ao observador uma escolha mental entre duas interpretações válidas: a silhueta de um vaso ou do perfil de duas faces humanas. Normalmente, o observador percebe apenas uma delas e somente após algum tempo acaba percebendo a segunda.
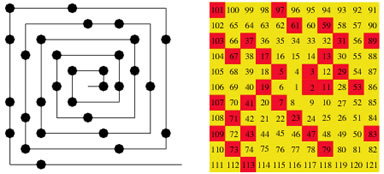
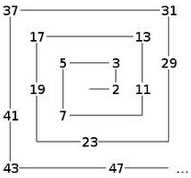
A espiral de números primos, também conhecida como Espiral de Ulam, é uma representação gráfica na qual os inteiros positivos são dispostos em forma de espiral, com os números primos sendo indicados de alguma forma ao longo dessa espiral.
Foi descoberta pelo matemático Stanislaw Ulam em 1963, enquanto rabiscava num papel, por estar entediado durante um encontro científico. Ele verificou que os números assinalados tendiam a agrupar-se segundo diagonais. Conforme imagem abaixo, onde os números primos estão assinalados em preto, as diagonais são perfeitamente visíveis, confirmando o padrão, que ainda permanece por explicar.
|
|
Escolha um número de 4 dígitos (exceto os números 1111, 2222, etc) e faça o seguinte:
1) Coloque os seus dígitos em ordem crescente
2) Coloque os seus dígitos em ordem decrescente
3) Subtraia o número menor do número maior
Repita os passos 1, 2 e 3 para o resultado, e assim por diante. O que acontece?
Vamos tentar com o número 8415.
Dígitos em ordem crescente: 1458
Dígitos em ordem decrescente: 8541
Subtraindo o menor do maior: 8541 - 1458 = 7083
Repetindo o processo com o número 7083:
8730 - 0378 = 8352
8532 - 2358 = 6174
7641 - 1467 = 6174
7641 - 1467 = 6174
7641 - 1467 = 6174 (a repetição continua....)
Incrivelmente, todos os números de 4 dígitos que não são múltiplos de 1111 acabam caindo nessa repetição.
|
|
|
|
Para acumular tanto dinheiro assim em apenas 30 dias, você deve fazer o seguinte:
- Guarde 1 centavo no 1º dia
- Guarde 2 centavos no 2º dia
- Guarde 4 centavos no 3º dia
- Guarde 8 centavos no 4º dia
- Guarde 16 centavos no 5º dia
... e assim sucessivamente, ou seja, no dia seguinte você deve ter sempre um total que equivale ao dobro do dia anterior.
Se você continuar fazendo isso durante um mês, ao final dos 30 dias você terá incríveis R$ 5.368.709,12! Mais de cinco milhões!
|
|
|
Seja para decorar a sua casa ou até para usar no pulso, já existem diversos de modelos de relógios que utilizam operações matemáticas. Logicamente, a ideia não é ficar fazendo cálculos para descobrir que horas são, mas estes relógios são uma bela opção decorativa, principalmente para os apaixonados por mamtemática. Confira alguns modelos que são produzidos atualmente.
|
|







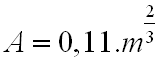
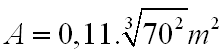













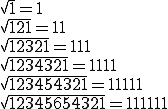





































.jpg)



Comentários
Obrigado por ter chegado até aqui! Se você gostou do nosso site,deixe aqui os seus comentário.
E que Deus vos abençoe!